从简单的神经网络开始。
在我们正式进入感知机的学习之前，我们可以先探索一下 Tensorflow 提供的交互式神经网络演示。
什么是单层感知机
单层感知机是最简单的神经网络，其由一个输入层全连接到一个输出层组成，如图 1 所示。
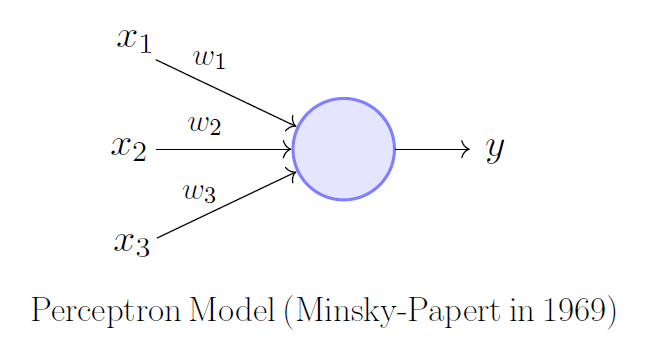
我们可以将上述模型表述为一次矩阵运算：
\[ y_0 = \mathbf{W}(\vec{x} + \vec{b}) \]
其中，\( \vec{x} \) 是感知机的输入；\( y_0 \) 是感知机的输出；\( \mathbf{W} \) 是每个神经元的权重；\( \vec{b} \) 是每个神经元的偏置值。不过，有些读者可能会指出：我们少了一个激活函数 \( \theta{}(\cdot{}) \)。技术上来说，\( y = \theta{}(y_0) \) 才是真正的感知机输出，其输出一个二元的结果。
一般而言，我们选择激活函数 \( \theta{}(x) = \frac{\mathrm{sgn}(x) + 1}{2} \), 即对于大于 0 的输入，结果为 1; 否则为 0.
用 Keras 创建并训练单层感知机
我们不妨实际构建一些简单的单层感知机。
线性分类问题
问题：如图 2，有以下数据点分为红蓝两类，请训练一个神经网络识别新的数据点应该分类到红色还是蓝色。
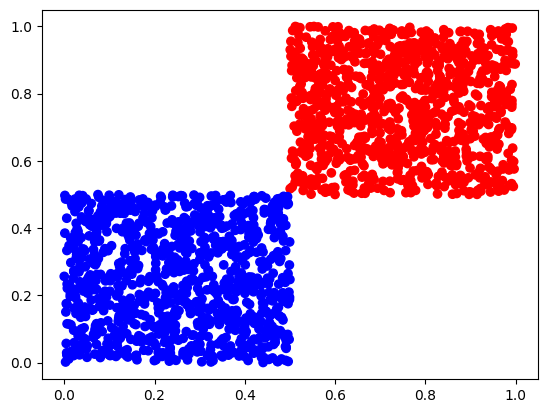
很容易能够看出，红蓝两组数据的明晰边界在 \( (0.5, 0.5) \)，而且可以通过一条直线 \( L[x, y]: y = 1 - x \) 划分成两个区域。
那么我们就直接进行代码的写。先搞一下数据生成部分：
import random
def generate_linear_group_a(count):
return [(0.5 + random.random() / 2, random.random() / 2 + 0.5) for _ in range(count)]
def generate_linear_group_b(count):
return [(random.random() / 2, random.random() / 2) for _ in range(count)]
linear_training_data_input = generate_linear_group_a(1000) + generate_linear_group_b(1000)
linear_training_data_output = [1 for _ in range(1000)] + [0 for _ in range(1000)]
然后是训练部分：
from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense model = Sequential() # 这里我们选择使用 ReLU 作为激活函数 model.add(Dense(1, input_dim=2, activation='relu')) model.compile(loss='binary_crossentropy', optimizer='rmsprop', metrics=['accuracy']) # 迭代 50 代，每次步进取 10 个样本 model.fit(linear_training_data_input, linear_training_data_output, epochs=50, batch_size=10)
最后简单跑个验证：
linear_test_data_input = generate_linear_group_a(100) + generate_linear_group_b(100) linear_test_data_output = [1 for _ in range(100)] + [0 for _ in range(100)] # 打乱测试数据的顺序 combined = list(zip(linear_test_data_input, linear_test_data_output)) random.shuffle(combined) linear_test_data_input[:], linear_test_data_output[:] = zip(*combined) # 执行模型评估 model.evaluate(linear_test_data_input, linear_test_data_output)
圆环分类问题
问题：如图 3, 有以下数据点分为红蓝两类，请训练一个神经网络识别新的数据点应该分类到红色还是蓝色。
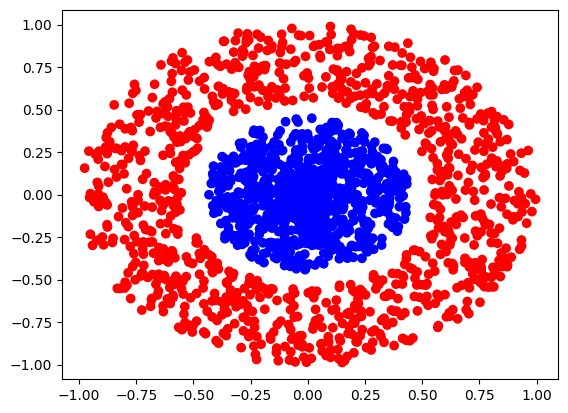
虽然我们仍然能够一眼看出来这两组数据的分界线 \(C[x, y]: x^2 + y^2 = 0.25\)，但是如果我们仍然使用 \((x, y)\) 作为输入的话，单层感知机将永远不会学会分辨这两组数据：因为不存在某个 \(L[x, y]: ax+by+c = 0\) 分隔两类数据。
不过，我们可以将直角坐标系转换为极坐标系来解决这个问题。如果给出映射函数 \( \varphi[(x, y)] = (x^2 + y^2, \mathrm{atan2}[y, x]) \)，那么我们就能将上述问题映射到图 4 所示的空间内：
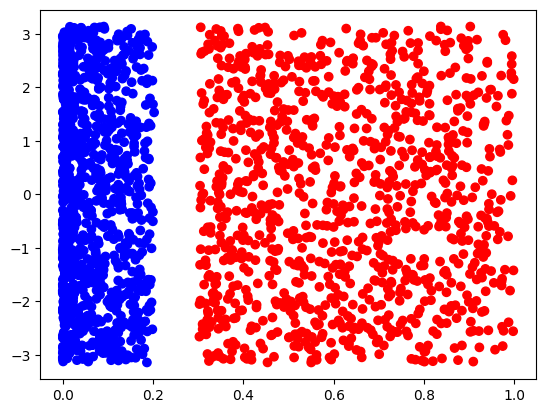
在这个空间内，就存在直线 \(L[r, \theta{}]: r = 0.25\) 分割两组数据了。
不过这回我们在验证该模型的时候需要意识到：由于我们是在 \(r-\theta{}\) 坐标系下训练的模型，当我们向模型输入数据时，也需要从 \(x-y\) 平面转换到 \(r-\theta{}\) 平面下才是正确的。
结论
单层感知机可以学会的分类问题是线性可分问题，即可以通过一个超平面将空间分割为两个半空间解决的分类问题。在实际的问题中，数据在当前的空间内可能并不是线性可分的，不过通过一些变换，有可能将这些数据映射到线性可分的状态。
在这一期我们留下了一些空窗，比如我们没有解释为什么要选择 binary_crossentropy 作为损失函数，也没有提 rmsprop 是怎么运作的。这些问题我们将在之后的探索中通过具体的样例理解。（对，我还没学会，所以现在就只能先用再说了。）
公式符号样式说明
- \( \mathbf{W} \) - 名字为
W的矩阵。所有矩阵都由粗体大写字母表示。 - \( \vec{x} \) - 名字为
x的向量。所有向量都由小写字母和箭头表示。 - \( y \) - 名字为
y的标量。所有标量都由小写字母表示。 - \( L \) - 名字为
L的超曲面。所有超曲面都由大写字母表示。 - \( f[x] \) - 名字为
f的函数，参数为标量x。为了避免混淆，所有的函数参数都使用方括号表示。这包括边界的描述。 - \( (x, y) \) - 由标量
x和标量y组成的二元组。为了避免混淆，所有元组都用圆括号表示。这包括横写的向量。
本期的笔记本文件可以在 http://dousha99.ysepan.com/ 获取。