Measurements! [0] – 重新理解示波器的带宽

你的测量究竟反映了什么？甚至，你的测量是否正确？

最近在工作上遇到了一些非常非常有趣的测量问题。当然，具体的内容我并没有权限透露，所以我们就构建一个场景吧。

有一个数字信号设备~~前来买瓜~~要求表 1 所述的电气特性。

项目	最小值	典型值	最大值
高电平阈值 (V)	-	2.9	-
低电平阈值 (V)	-	0.3	-
高电平保持时间 (ns)	7.1	-	-
低电平保持时间 (ns)	7.1	-	-
时钟频率 (MHz)	-	64	-

表 1 设备的电器特性

现在的问题是：我们怀疑输入该设备的信号不满足上述电器特性要求。我们能否通过一部 100MHz 带宽的示波器说明这个问题呢？

示波器的标称带宽

通常，示波器的有效带宽是示波器的模拟前端带宽和探头标称带宽中最小的那个。为了方便讨论，我们就假设示波器和探头的带宽都是 100MHz.

但是有趣的是（尤其是如果你在实验室无事可做的时候），如果你尝试用这个组态去测量 200MHz 的正弦信号，示波器上仍然会有波形产生；而且如果使用示波器的测量功能，仍然能够正确地得到信号频率为 200MHz 的结果——当然，波形幅值会不对。那么，为什么示波器厂商不干脆尝试在高频自动放大幅值，这样就能把自己的示波器带宽标得更高了呢？

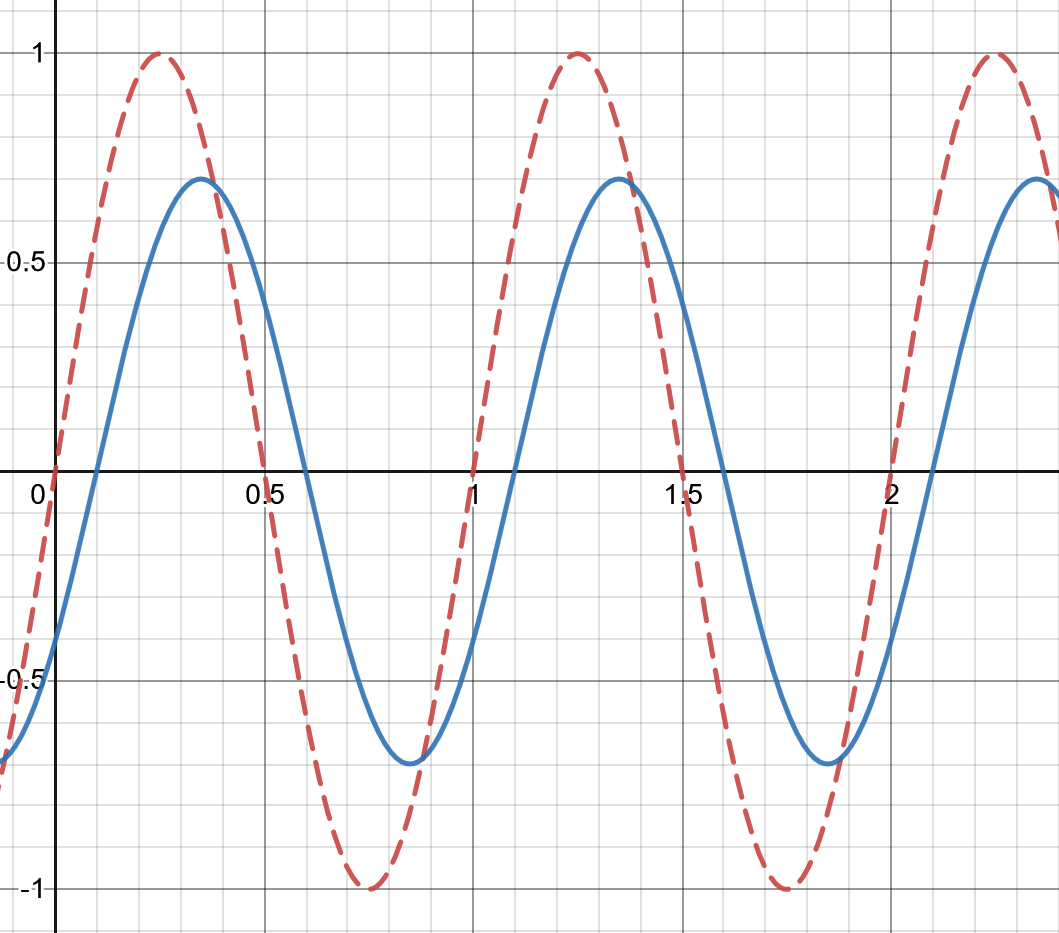
这是因为示波器的「带宽」并不仅仅和「多高频率的正弦波可以进入仪器」有关，还和上升沿时间有关。如图 1 所示，红色虚线为真实波形，蓝色实线为示波器波形。由于输入信号的频率大于示波器带宽，示波器模拟器前端的上升和下降时间均比实际波形的上升和下降时间要长，导致幅值减小，同时显示的波形滞后于实际信号。但是由于上升和下降仍然最终发生了，所以示波器仍然可以测量出大差不差的频率。

不过应注意到：超过标称带宽的测量最多算定性测量，即测量是否有这么一个信号存在。任何更精确的测量都是没有意义的。

方波的频率与带宽

在数字信号系统中，传输的信号通常使用方波。这意味着一个非常有趣的事实：数字信号传输所要求的带宽可能实际上非常大，哪怕在纸面上写出的频率并不是很高。

考虑理想 1Hz 方波：\(f(t) = \begin{cases} 1 & \sin(2\pi{}t) \ge 0 \\ 0 & \sin(2\pi{}t) < 0 \end{cases}\). 这个信号表面上是 1Hz 的带宽，但实际上需要无穷大的带宽才能产生。

对信号进行傅里叶变换得

\[g(t) = \mathcal{F}(f(t)) = \frac{2}{\pi}\sum_{i=0}^{\infty}{\frac{1}{2i+1} \sin(2\pi(2i+1)t)} + 0.5 \]

在现实场景中，我们不可能生产任何具有无穷大带宽的设备或链路，所以实际传输的信号是若干次谐波组成的近似方波的信号 \(h(t, m)\). 图 2 是 \(h(t, 5)\) 的图象，其带宽（最高次谐波频率）为 11Hz.

\[h(t, m) = \frac{2}{\pi}\sum_{i=0}^{m}{\frac{1}{2i+1}\sin(2\pi(2i+1)t)} + 0.5\]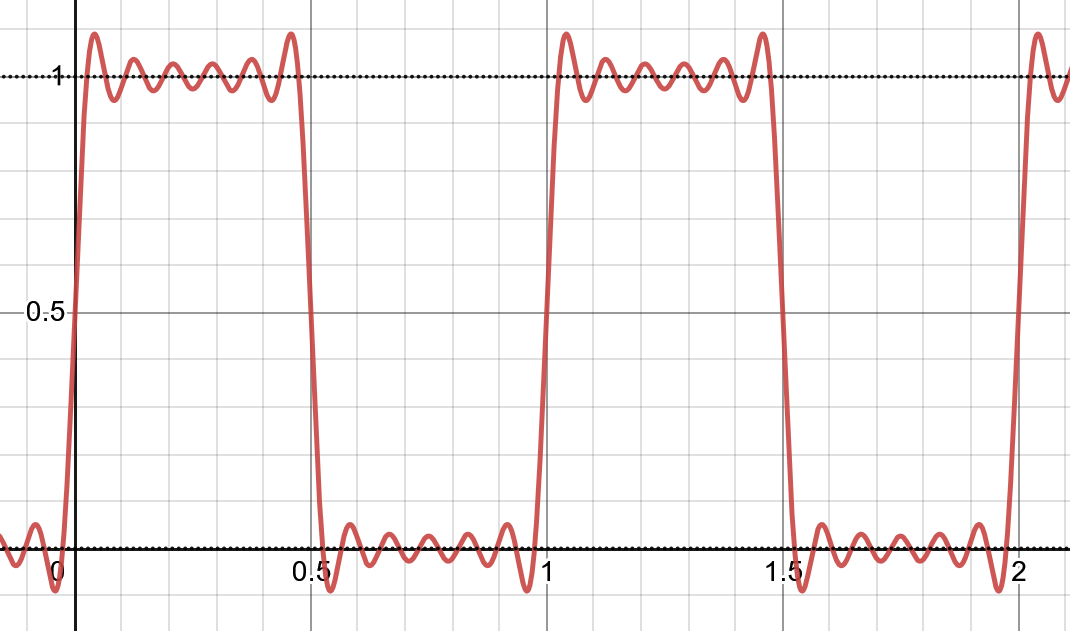

这产生了「上升沿时间」这样一个概念。在工程应用上，定义信号幅值从 \(0.1\) 到 \(0.9\) 所经过的时间为信号的上升沿时间。图 3 为 \(h(t, 5)\) 的图象，其上升沿时间约为 \(0.0372\) 秒.

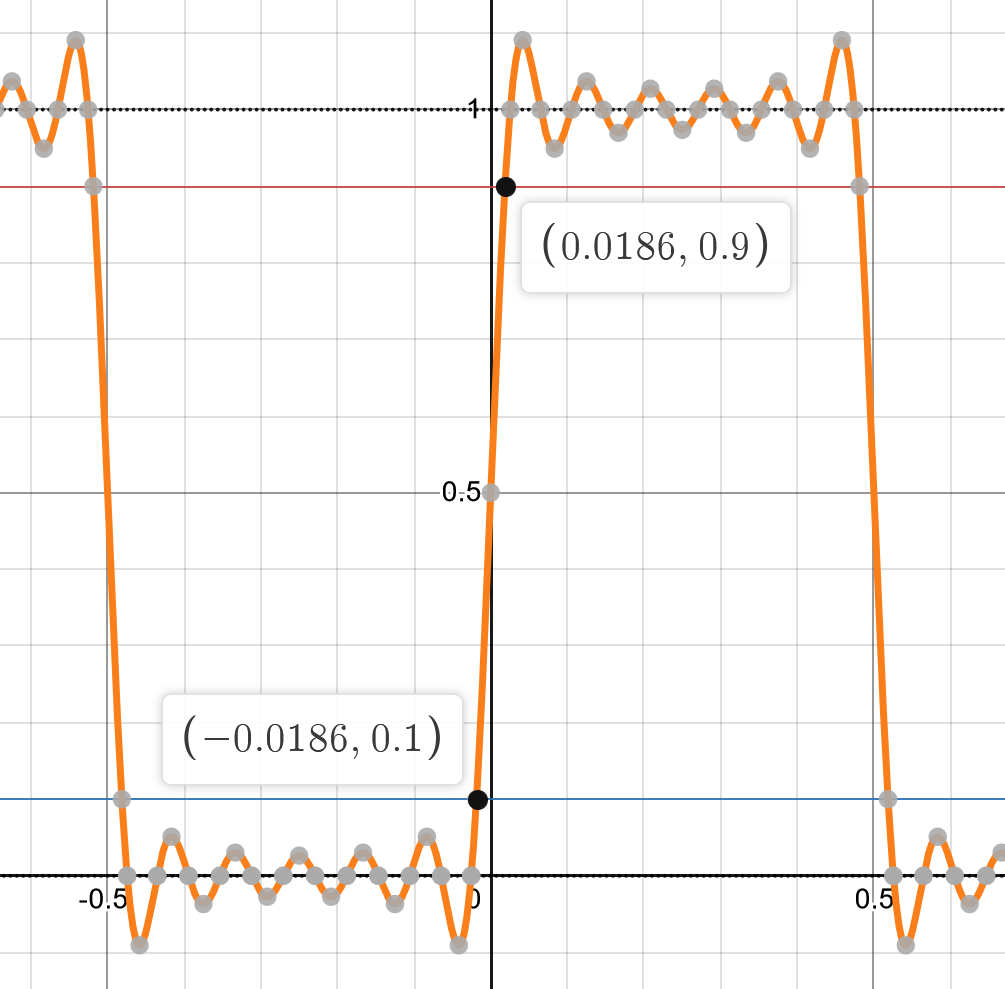
示波器的波形

如果我们的示波器带宽不足，那么示波器的波形将不再反映真实信号。我们仍旧以 \(h(t, 5)\) 为例。设示波器的带宽为 2Hz. 按简单一阶低通滤波器 (-20dB/dec) 计算衰减系数 \(v(f)\) 如表 2 所示。

频率 (Hz)	频率 (\(\log\frac{f}{f_{3\mathrm{dB}}}\))	衰减系数 (dB)	衰减系数 (1)
1	-0.301	0	1
2	0	-3	0.5
3	0.176	-3.52	0.44
5	0.397	-7.94	0.16
7	0.544	-10.88	0.08
9	0.653	-13.06	0.05
11	0.740	-14.8	0.03

表 2 衰减系数的值

将衰减系数代入 \(h\) 得到示波器波形表达式 \(u(t)\). 图 4 是 \(u(t)\) 的图象，可以看到这个波形更近似于「平坦」一些的正弦波，而不是之前看到的更不平坦的图象。

\[u(t) = \frac{2}{\pi}\sum_{i=0}^{5}{\frac{v(2i+1)}{2i+1}\sin(2\pi(2i+1)t)} + 0.5 \]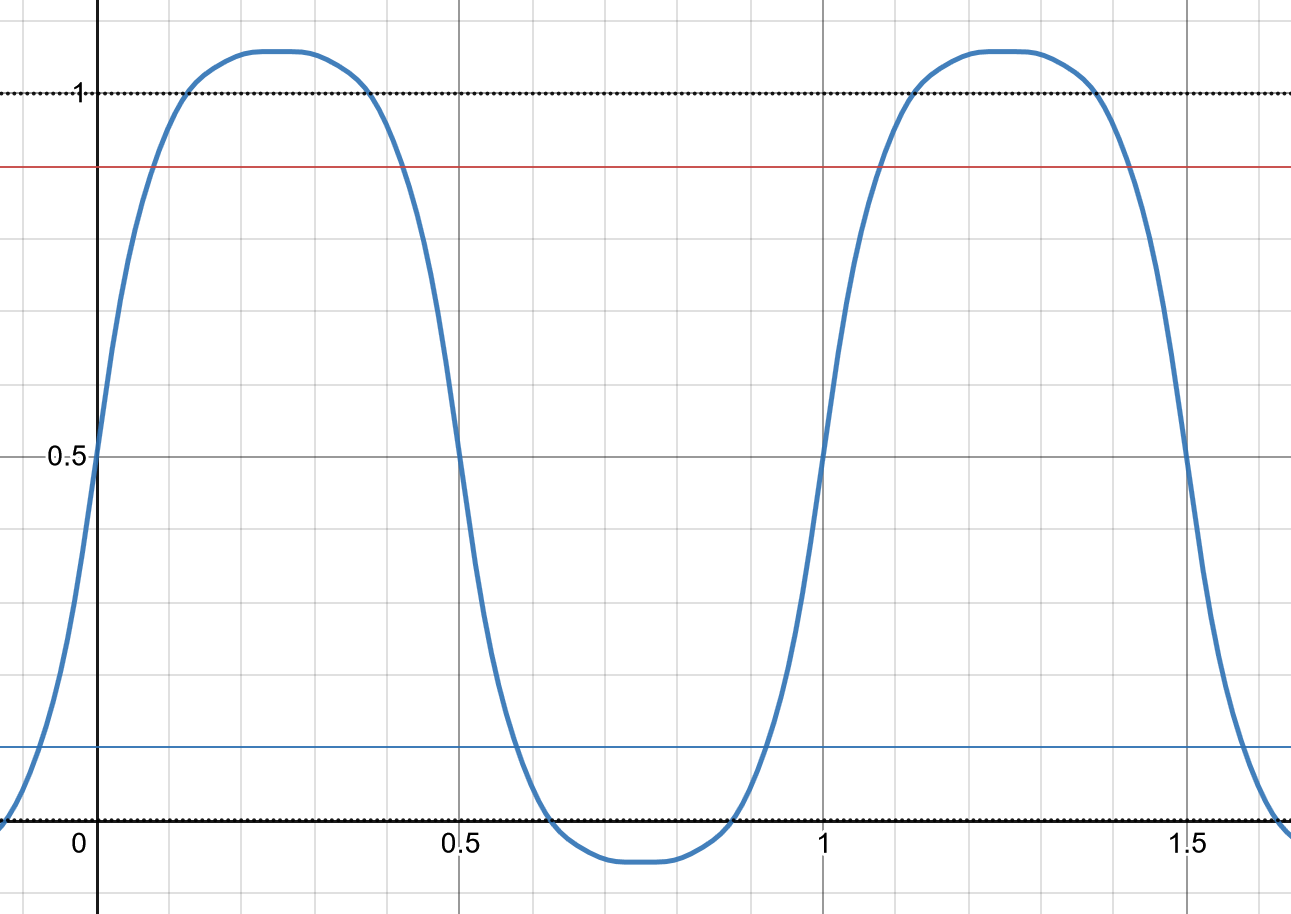

对定量测量的影响

如果我们不知道这一问题，认为图 4 已经「算是正常的方波信号」的话，这会对我们的测量产生怎样的影响呢？我们将真实信号用橙色虚线表示，示波器信号用蓝色实线表示，一起绘制，如图 5 所示。

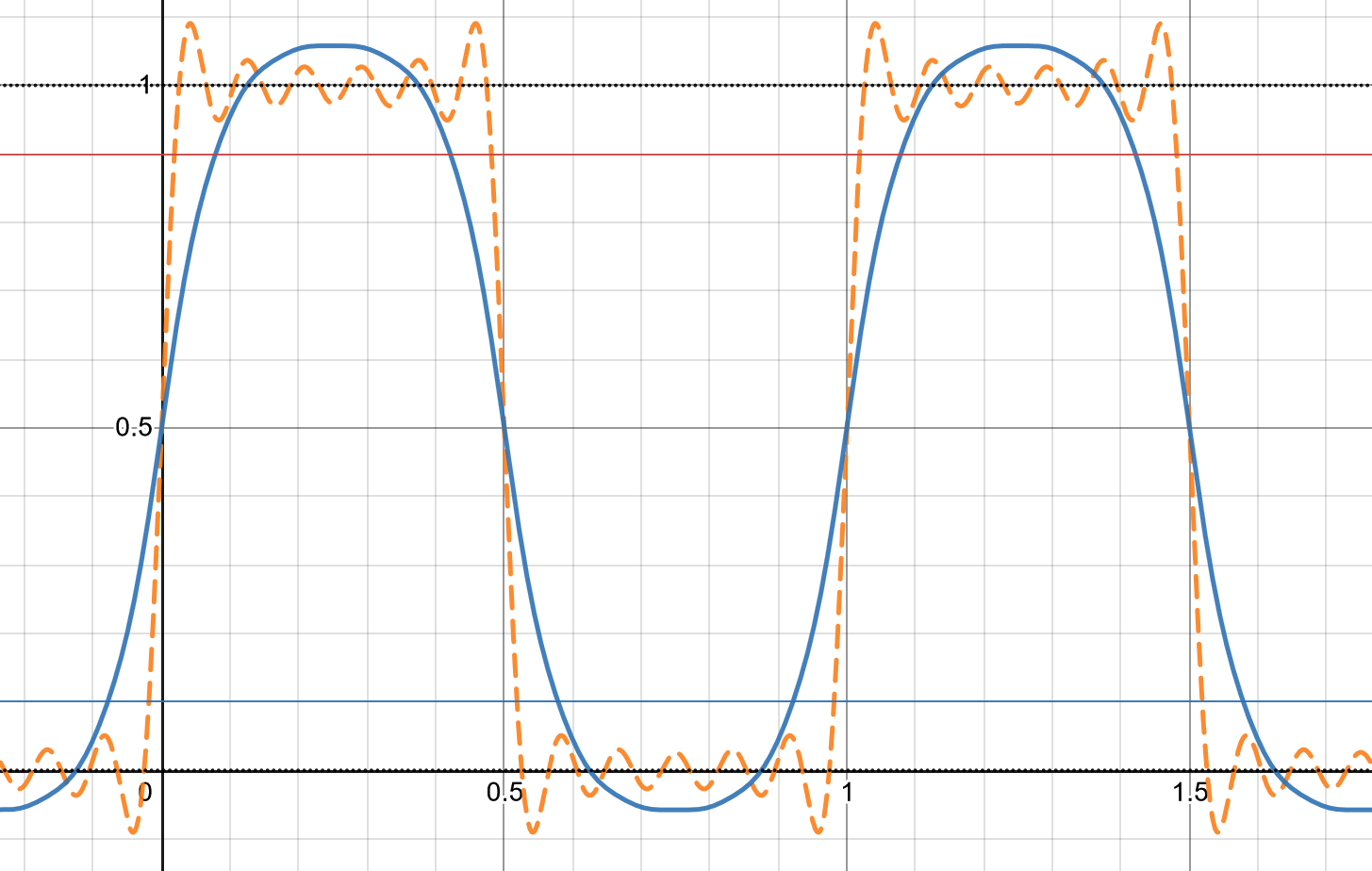
首先我们就可以注意到幅值不对：示波器波形的高电平比实际信号的高电平要更高；低电平比实际信号的低电平要更低。

如果我们测量上升沿时间和下降沿时间，如图 6 所示，示波器的上升沿时间为 \(0.1572\) 秒，相对误差达到了 322.58%!

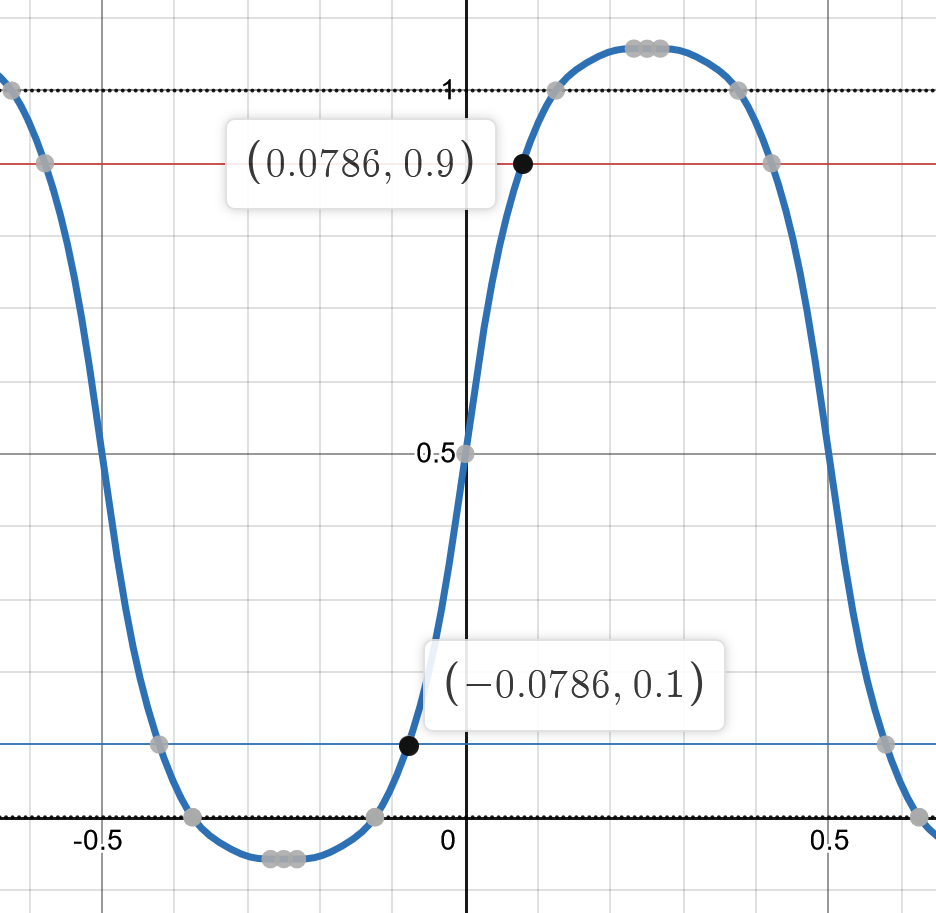
对于低电压应用或者高速设备应用，这种测量的误差很有可能会导致该通过的设计被标记为不通过；或者不应通过的设计被标记为合格。回答在开始提出的问题：100MHz 的示波器不能用于检查 64MHz 的时钟信号。在这种非常高的时序要求下，我们可能需要上 GHz 的带宽才能进行有效的测量。

能通过数学解决这种问题么？

如果我知道这种现象的存在，但是限于条件我没法使用具有足够带宽的测量仪器，我能否通过额外的计算来还原实际信号呢？

答案是：如果这种事情可以被做到，那么示波器就会内建这个功能。实际信号比我们用数学公式模拟出来的结果要更为复杂——在这个模型里面，我们没有计入真实测量过程中的噪声、探头阻抗对信号的影响等等。所以，不要想着通过非常有趣的数学 trick 做出自欺欺人的计算。老老实实选择合适的测量设备，做出正确的测量有益身心健康。

估计信号带宽

在实际工程上，我们通常不需要坐下来做各种乱七八糟的计算。一个简单的估算方法是 \(\frac{0.45}{T_e}\), 即信号带宽是 0.45 除以边沿时间（单位为秒）。按照这个估算方法，\(h(t, 5)\) 的带宽约为 12.096Hz, 略微大于实际值。

至于这个估算方法是怎么来的？经验值。由于这是经验值，所以每个人取的常数都可能不太一样：有的取 0.3, 更常见的是 0.35, 以及 0.45. 那么如果我们需要更精确的计算，应该怎么办呢？

那就到了愉快的解级数时间！基本思路是：对于一个已知基础频率的方波信号，解算出使得上升沿时间满足要求的级数项数，则最高次项的频率即为所需带宽。具体的计算过程留作练习。（或许可以写一个 Mathematica 脚本来求解，但我没学过 Mathematica 所以没法整活 ¯\_(ツ)_/¯ 或者其实已经有人写过 MATLAB 程序来干这事了，工程嘛，数值计算不寒碜。）

估计测量所需带宽

对于数字示波器而言，其上升沿分辨率同样遵循估算。而测量误差可以通过平方和估计，即最差读数为 \(\sqrt{信号上升沿时间^2 + 示波器上升沿时间^2}\). 最差读数与实际值的相对误差感觉差不多（比如小于 5%）的时候就可以了。

Measurements! 是讨论测量示波器使用的一般原理和要点的系列文章。很多人觉得示波器不就地线一接、探头一插就结束的事情，但实际上并非如此——正确的测量远不止把线接好、扭两下旋钮那么简单。